Forschungsgruppe Zahlentheorie
Die Forschungsgruppe Zahlentheorie beschäftigt sich mit Verbindungen der Zahlentheorie zur Geometrie und mit der analytischen Zahlentheorie. Sie wird von Prof. Habegger und Prof. Le Boudec geleitet.
Eine interessante Frage ist, wie viele Punkte mit ganzzahligen oder rationalen Koordinaten auf einer ebenen Kurve liegen. Oder kann die Summe zweier Kubikzahlen, wie z.B. 1, 8, 27 usw., wieder eine Kubikzahl sein? Auch ein solches Problem lässt sich mit geometrischen Werkzeugen untersuchen.
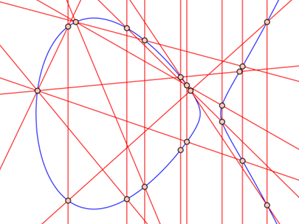
Besonders elliptische Kurven sind im Fokus der Forschung. Mittels der rechts abgebildeten Sehnen- und Tangentenkonstruktion lassen sich zwei Punkte zu einem dritten Punkt «addieren». Diese «Addition auf der Kurve» verbindet Geometrie und Arithmetik und ist ein mächtiges Werkzeug, um die elliptische Kurve zu studieren. Sie spielt in Anwendungen der Kryptographie eine wichtige Rolle.